Statistical Functions

BernoulliDist

Returns a value of 1 or 0; the argument indicates how frequently the value of 1 is returned on a percentage basis. For example: BernoulliDist(0.7) implies a value of 1 is returned 70% of the time.

BernoulliDist(Probability)

BetaDist

Returns the cumulative Beta probability density function between the minimum and maximum values that you supply. The BetaDist function is commonly used to study variation in a percentage across samples.

BetaDist(A,B,Min, Max)

Between

Provides a uniformly-distributed number between the minimum and maximum values that you supply. For example, if you use Between(10,20), the value returned has an equal probability of being any real number from 10 to 20, both numbers inclusive. For example: 12.5 or 16.413.

Between(Min,Max)

BetweenNorm

Provides a Normal random variable between a minimum and maximum value. For example, if you use BetweenNorm(10,20), the value returned is more likely to be 14, 15, or 16, and seldom 10 or 20.

The BetweenNorm function is the same as the NormDist function except that the mean and standard deviation are calculated automatically according to the minimum and maximum values that you provide. Also, the value returned is always inside the specified range.

BetweenNorm(Min,Max)

BinomDist

Models drawing or selecting items from a pool, where N is the number of items in the pool and Probability is the probability of each item being successfully drawn.

BinomDist(N,Probability)

ErlangDist

Generates random values where N is the mean distribution and B is the variance. Both N and B must be greater than zero and N is an integer. (The Erlang distribution is a subset of the Gamma distribution.)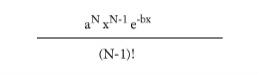

ErlangDist(N,B)

ExponDist

Returns a pseudo-random value from the Exponential distribution. The value is always positive and is explained completely by specifying a single argument, the Mean.

For example, if you specify ExponDist(15), the values, over time, tends to cluster around 15. Spikes of much larger values are always possible with the exponential distribution, so the Max argument is provided to truncate the distribution. If Max is supplied, no value larger than Max is returned. If, after trying 50 samples, no value is obtained less than Max, the value from the uniform distribution between 0 and Max is returned, and no warning is issued. This can happen with poorly chosen Max values, such as a value less than Mean.

The function used to calculate the value is:

Mean * -ln(1-x)

where ln is the natural logarithm function and x is a pseudo-random value from the uniform distribution between 0 and 1.

ExponDist(Mean, Max)

GammaDist

Generates random values with the following density: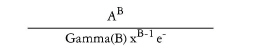

GammaDist(A,B)

LogNormDist

Is the logarithmic normal distribution. The first parameter is the mean and the second is the variance (deviation squared).

LogNormDist(Mean,Deviation)

NormDist

Provides a Normal random variable indicated by its mean and its standard deviation.

NormDist(Mean,Deviation)

NormSDist

Provides a standard normal random variable where the mean is 0 and the standard deviation is 1. This function does not take any arguments. The value is generated within the distribution curve.

NormSDist()

PercentTrue

Returns true Num% of the time. For example, PercentTrue(95) becomes true 95% of the time

PercentTrue(Num)

PercentFalse

Returns false Num% of the time. For example, PercentFalse(95) becomes true 95% of the time

PercentFalse(Num)

PoissonDist

Is a limiting form of the Binomial distribution when, in the Binomial expression, N tends to infinity and Probability tends to zero at the same time. Exponential interarrivals are the same as Poisson arrivals.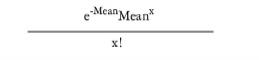

PoissonDist(Mean)

ProportionalDist

Generates a random proportional distribution. Let Sum = Num0 + Num1 + ... + Num(n); 0 <= n <= 11; Num0, Num1, ..., Num(n) >= 0. If Sum = 0, return -1, else return the integer value i, 0 <= i <= n, with the probability of Num(i)/Sum.

ProportionalDist(Num0,Num1,[...])

Random

Provides a random real number between 0 and 1, based on a uniform distribution.

Random()

TriangleDist

Returns the value of a triangle-shaped distribution. The arguments Min and Max determine the smallest and largest values to return. Mode returns the most likely or peak value of the distribution.

TriangleDist(Min,Max,Mode)

WeibullDist

Typically used for reliability analysis. It takes two parameters, A and B. Both must be greater than 0. Generates random values with the following density:

ABx^B-1exp(-Ax^B)

WeibullDist(A,B)

WeibullStdDist

Is the Weibull distribution that takes two parameters. The first parameter is the shape and the second is the scale. It is the same distribution as WeibullDist(A, B) where A = 1 / (scale^shape) and B = shape.

WeibullStdDist(Shape,Scale)